TL;DR

- Challenge Setup: We are an established Man-in-the-Middle between Alice and Bob
- Key Discoveries: To initially exchange a shared key, the Diffie-Hellman Key Exchange is used and the OTPs are calculated via the KDF SP800 108 Counter Mode
- Vulnerability: Diffie-Hellman Key Exchange is vulnerable for a Man-in-the-Middle attacker and SP800 108 Counter Mode breaks by the wrong usage of the underlying PRF
- Exploitation: Just exploit the vulnerable crypto components :P

1. Introduction

We are given some Python files simulating a series of communication exchanges between Alice and Bob. Luckily enough, we are already an established Man-in-the-Middle, so we can intercept, modify and drop any communication between these two parties. The goal of the challenge is to modify the exchanged messages so that Bob will receive the message with content like allgoodprintflag from Alice. The twist of this challenge lies in the used crypto algorithms like the used key derivation function (KDF) SP800 108 Counter Mode and its underlying primitives.

2. Reconnaissance

The communication starts with the popular Diffie-Hellman Key Exchange using a secure group. After both parties calculated the shared key Alice and Bob agree on one of the three NIST certified pseudo random functions (PRF) HMAC, CMAC and KMAC, for the KDF. Both parties randomly select a nonce and exchange these to have a common KDF context. After that, the shared key, the chosen PRF, the common context and some hardcoded string are used to derive a common key out of the KDF algorithm SP800 108 Counter Mode. Alice then sends Bob a message wearecompromised because she is already suspicious about the connection, as the description tells us. The only way to receive the flag is by somehow making sure Bob receives allgoodprintflag as a message.

3. We are the man in the middle

At first, we want to make sure we get to know the shared secret being calculated via the Diffie-Hellman Key Exchange. Both parties calculate the same shared secret \(K = g^{ab} \bmod P\) through modular exponentiation with a prime P, which can then be used for symmetric encryption:

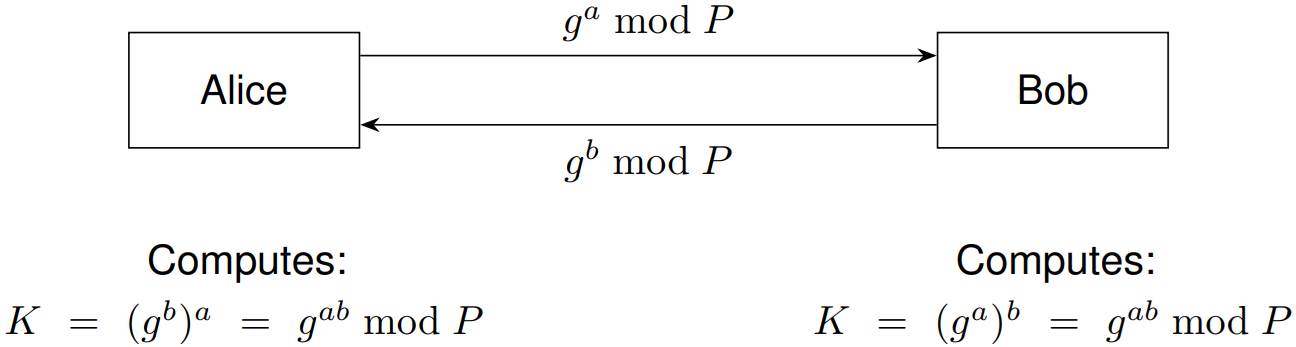
But this key exchange is highly vulnerable to a Man-in-the-Middle attack. We intercept the communication, inject our public key and thus get for each party another shared secret we can also calculate:

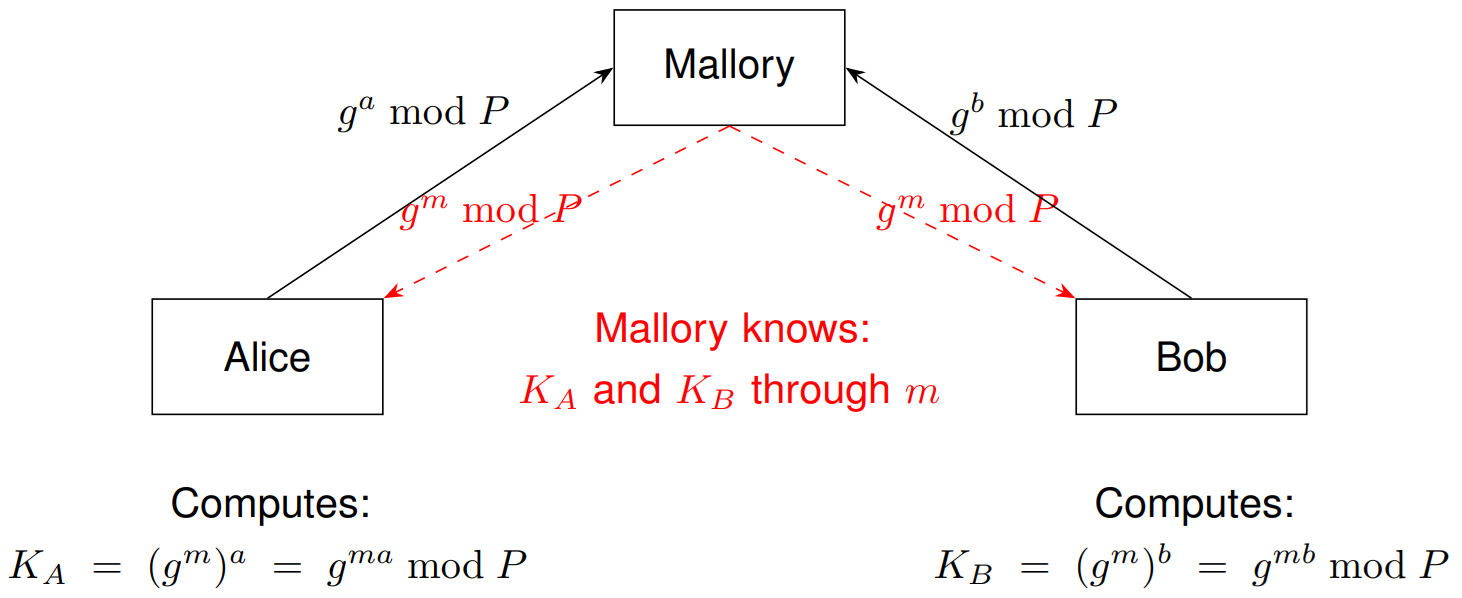
As in most CTF challenges, there is not only one way to solve a problem. The Man-in-the-Middle can also force a trivial shared secret K=1 by simply sending P-1 to each party. The reason for this is the following equation holding for any prime P:

This also means Alice and Bob are actually calculating

with k being their private secret. This results in the shared secret K:

The probability of both parties choosing even exponents is:

4. Deriving some flags

Now that we know the shared secret, we can decrypt every message Alice and Bob send each other via the KDF-derived OTPs, as we can calculate these ourselves. But this is not enough for the challenge, we need to influence the output and thus the derived OTPs.

There is a NIST document describing the algorithm for SP 800 108 in detail. It is basically a loop like the following:

for i = 1 to n, do
    K(i) = PRF(K, [i] || label || 0x00 || context || [L])
    result = result || K(i)

[x] just means the integer is padded to 4 bytes. The label is the hardcoded string keygen_for_secure_bagdrop and L is the length of the derived key.

Having a look at the used PRFs, one of them seems more suspicious than the others. HMAC and KMAC internally use hash functions, so they are not that interesting for us, as predicting the output of a hash function is nearly impossible. You would have to brute force the appropriate input for some desired output. But CMAC is different, being based on the symmetric crypto algorithm AES and the Cipher Block Chaining Mode (CBC).

There are some nice explanations out there on how the AES-CMAC works. As we know the shared secret from the Diffie-Hellman Key Exchange, we also know the key used for AES, so we can easily reverse the process of CMAC. For the KDF context of each party, we have control over exactly the second half (for Alice) and the first half (for Bob). So in both cases, we control 16 bytes for the OTP generation.

We will go for the first part of the context of Bob influencing his OTP. The reason for this is that at the time of intercepting the nonces and modifying the one dedicated to Bob, we already know the nonce for Alice and thus can calculate her OTP, which will be important later.

To proceed, we need some formulas. Each \(M_i\) got its own block, so overall there are 5 blocks in the CMAC. \(K_{IN}\) is the shared secret key from the Diffie-Hellman Key Exchange used as the encryption key for AES. \(M_i[x:y]\) represents all of the bytes of \(M_i\) starting with index x until index y. K' is the AES subkey we can easily calculate via the shared key and T is the target OTP we want to forge. The green highlighted parts \(M_2[14:16]\) and \(M_3[0:14]\) are the first half of the context we can control:

Now we can just rearrange and substitute the formula as follows:

Now we have on both sides of the equation parts we can control. We just need to brute force \(M_2[14:16]\) until the two bytes \(M_3[14:16]\), which we are not able to control, are the correct ones. There might be the rare case in which we can't fulfill the equation, although we tried all of the \(2^{16} = 65535\) variations. In this case, we need to repeat the whole exploit. Because of the equation holding, using the calculated context will result in our selected OTP target T. Before calculating the context for Bob, we need to determine our OTP target T. This can be done using the calculated \(OTP_A\) from Alice, the hardcoded allgoodprintflag string \(m_{flag}\) and the hardcoded wearecompromised string \(m_{compromised}\):

With this information and the derived equation, the implementation is straightforward:

from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes, bytes_to_long
from Crypto.Util.py3compat import bord

def xor(a, b):
    return bytes(x ^ y for x, y in zip(a, b))

def _shift_bytes(bs, xor_lsb=0):
    num = (bytes_to_long(bs) << 1) ^ xor_lsb
    return long_to_bytes(num, len(bs))[-len(bs):]

def get_aes_cmac_subkey(key):
    L = AES.new(key, AES.MODE_ECB).encrypt(b"\x00"*16)

    const_Rb = 0x87

    if bord(L[0]) & 0x80:
        _k1 = _shift_bytes(L, const_Rb)
    else:
        _k1 = _shift_bytes(L)
    if bord(_k1[0]) & 0x80:
        _k2 = _shift_bytes(_k1, const_Rb)
    else:
        _k2 = _shift_bytes(_k1)
    return _k2

def forge_nonce_for_target(key, T, ctx_second_half):
    c = AES.new(key, AES.MODE_ECB)
    aes_subkey = get_aes_cmac_subkey(key)

    ctx_first_half_2_16 = None
    testing_int = 0
    ctx_first_half_0_2 = b''

    while testing_int <= 0xFFFF:
        ctx_first_half_0_2 = testing_int.to_bytes(2, 'big')
        attempt = xor(
            c.decrypt(
                xor(
                    c.decrypt(
                        xor(
                            xor(
                                c.decrypt(T), b'\x00\x80\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'
                            ), aes_subkey
                        )
                    ), ctx_second_half[2:16] + b'\x00\x00'
                )
            ), c.encrypt(
                xor(c.encrypt(b'\x00\x00\x00\x01keygen_for_s'), b'ecure_bagdrop\x00' + ctx_first_half_0_2)
            )
        )

        if attempt[-2:] == ctx_second_half[0:2]:
            ctx_first_half_2_16 = attempt
            break
        testing_int += 1

    # ctx_first_half[0:2] || ctx_first_half[2:16]
    return ctx_first_half_0_2, ctx_first_half_2_16

The returned value from the forge_nonce_for_target function is the calculated first half of the context from Bob. After sending Bob the forged nonce, he will receive allgoodprintflag and we get the flag dach2025{But_n1st_said_it_was_fine?!???_15f7a069}. The NIST once proposed CMAC as one of the PRFs you could use together with the KDF SP800 108 Counter Mode. But when some employees from Amazon reported some security issues with this combination, NIST revoked it and added a precise description of the attack in the appendix of their publication.

5. Mitigation

The first problem is the usage of the Diffie-Hellman Key Exchange without any authentication. By using signatures or a public key infrastructure (PKI), the parties could have validated each other's identities, preventing the Man-in-the-Middle from sharing their keys or manipulating the key exchange. For the KDF part, obviously you shouldn't use SP800 108 Counter Mode with CMAC but with for example HMAC. Overall, you must be very careful when any crypto modules come into play. Although the Python library cryptography wasn't used in this challenge but instead pycryptodome, they got a great note in their documentation to KDFs:

[...] this module is full of land mines, dragons, and dinosaurs with laser guns.

76. Flag

dach2025{But_n1st_said_it_was_fine?!???_15f7a069}